走時曲線について①

記録波形の初動を読み取れたら、その読取値でいよいよ走時曲線を作成します。

ここからが、弾性波探査のハギトリ法解析を進めていく第一歩です。

これまで何度も言葉として登場している走時曲線ですが、あまり馴染みがないと思います。

走時曲線とは、起振ごとの初動読取値を、横軸を距離（測点）、縦軸を時間（初動読取値）としてプロットしたグラフになります。

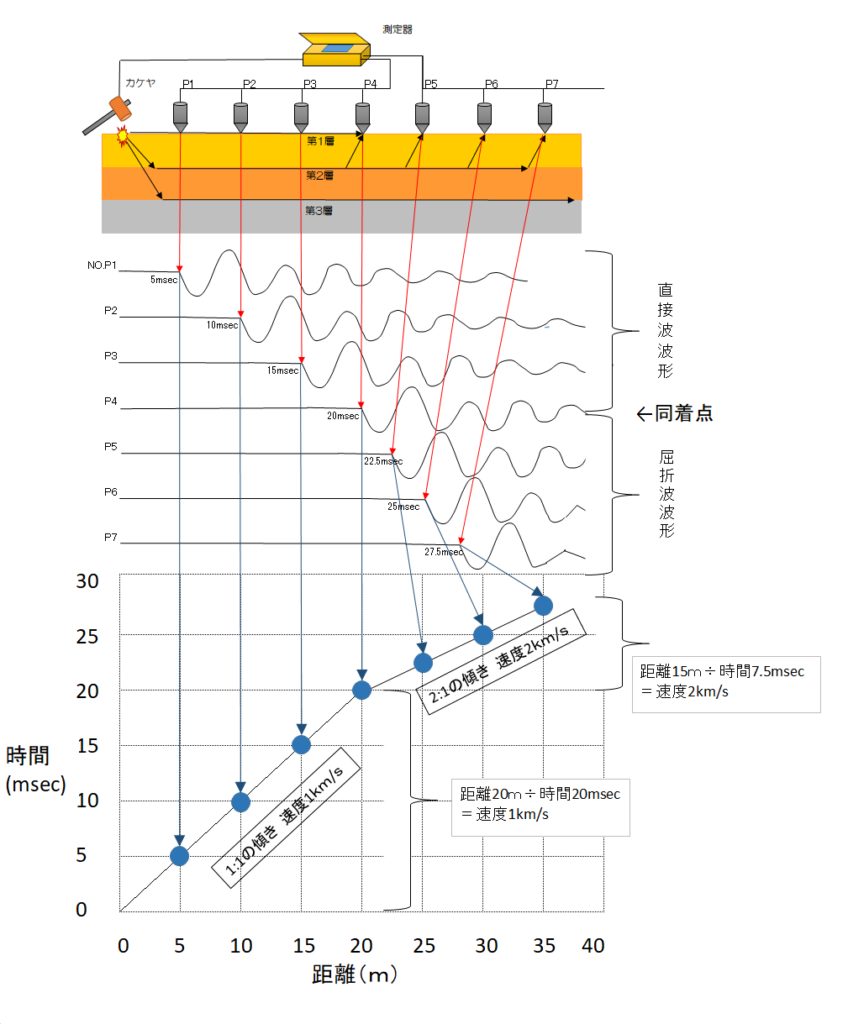
上図は、7ヶの地震計を5ｍ間隔で設置し、0ｍ地点で起振した際の初動読み取りと、その読取値を走時曲線にした模式図です。

初動読取と走時曲線の相関が理解しやすいでしょうか。

さて、これで何が分かるのか？そもそもなぜ走時曲線を作成するのか？というと、弾性波探査の屈折法解析は多くの計算式を用いた難解なものであるため、それを図式解法で単純化し視覚的に分かりやすくするためです。

地盤の硬軟は、地盤を伝わる弾性波の速度で表すので、速度値を求めるのが走時曲線の第一の目的です。

速度を求めるには「距離÷時間＝速度」の計算をしなくてはなりませんが、横軸＝距離、縦軸＝時間のグラフの傾きは速度になることから、図上の傾きに定規を当てるだけで速度を求めることができます。

上図を例に用いると、起振点0ｍから地震計P4までは同じ角度の傾きです。

この傾きに定規をあてると、縦横１マスずつ　1：1の角度であり、速度は１(km/s)となります。

計算では、距離20ｍでかかった時間は20msec。20m÷20msec＝1km/s　と、求まります。

さて、P4から先は傾きが変わっています。波が、表層とは速度値の異なる地層を伝わっているためです。

このP4が、表層を伝播する直接波と、下部の硬い層からの屈折波とが同着する地点です。

P1～P4は直接波が先着、P4～P7は屈折波が先着しているということです。

では先程と同様に、傾きに定規をあてると横2マス・縦1マス　2：1の角度であり、速度は２(km/s)となります。

計算では、P4（20ｍ）からP7（35ｍ）まで距離15ｍで、かかった時間は7.5msec。15ｍ÷7.5msec=2km/s　と、求まります。

各速度値を上図にあてはめると、第1層はVp=1km/s、第2層はVp=2km/sであると解析されました。

（厳密に言えば、まだこの段階では真の速度値ではありません）

今回は分かりやすくするため受振点・起振数はごく少数で、地盤モデルも単純な水平2層構造ですが、実際には受振点は数十～数百に及び、起振点も多くなります。地形の変化や地層の数・形状ももっと複雑です。

これらを全て計算すると膨大で難解な作業になりますが、図式解法なら迅速かつ簡便に速度を求めることができます。

ここまでで速度値が求まりましたが、さらに速度層の数、各速度層の速度値、層厚、形状まで、走時曲線の図上で解析していきます。

走時曲線は、屈折法弾性波探査・ハギトリ法解析の要といえるのです。