News/Pickup
-

別府温泉
今年の社員旅行は別府温泉♨♨♨
伊丹空港から飛行機で50分ほど。あっという間です。
昼に大分空港に到着し、レンタカーでまずは海鮮BBQ!

ホテルのチェックインまで時間があるので杵築市の旧城下町を散策。


ここで有名なのは「酢屋の坂」と「塩屋の坂」二つの坂道が相対しているサンドイッチ型の城下町。
道の両側に武家屋敷の歴史的な門塀が並ぶ、きれいな石畳の坂道は素晴らしい。
着物の似合う歴史的町並みに選ばれただけあって、とても絵になります。
杵築城に行こうと思ったが、道がわかりにくい・・・
杵築城の模擬天守は資料館になっていて、ここから眺める守江湾や国東半島の輪郭は美しかったです。


日本で一番小さいお城らしい。
別府市に移動。町のあちこちから温泉の水蒸気が立ち昇る、これぞ温泉地という景観です。
有名な地獄めぐりへ。時間の都合で、7つある地獄のうち海地獄と鬼石坊主地獄を見物。


コバルトブルーの美しい池の海地獄。池の奥の間欠泉が勢いよく吹き上がっており迫力がある。
泥沼から源泉が沸き上がる様子が坊主頭に見える鬼石坊主地獄
夕方になりホテル白菊にチェックイン。ウエルカムスイーツバイキングで一息ついて、さっそく温泉へ。
硫黄の匂いは控えめでさらっとした泉質。長湯できる感じで良かった♨
夕食は関サバや豊後牛など大分県の味覚満載🐟

翌日は、別府市郊外の鶴見岳にある別府ロープウェイへ。始発早々に行ったが中国の団体観光客でにぎわっていました。


別府市街の展望。上から噴気が見れるかと思ったがそうでもない。ロープウェイ乗り場下の焼酎館で酒をいっぱい買う(笑)
昼食は大分名物とりてん定食。発祥の店に行こうとしたけど1時間半待ち!別府駅前の別の店で食べました。衣がザクザクしてて唐揚げとは全然違う!
駅前にある、別府観光の生みの親と言われている油屋熊八氏の銅像は思ったよりでかかった。
空港への道中、有名な湯布院の湯の坪街道へ。平日なのに観光客やバスでごった返すしてるのは驚きでした。


イギリスの村をイメージした、小さいながらも手の込んだ小テーマパーク・フローラルヴィレッジは女の子が喜びそうなファンタジー感!フクロウの森やヤギに餌あげられたりと個性的な店が並んでました。
大分空港から帰路。親睦を深めた社員旅行でした。
-

物理探査のアレコレ 屈折法弾性波探査 その3
走時曲線について①
記録波形の初動を読み取れたら、その読取値でいよいよ走時曲線を作成します。
ここからが、弾性波探査のハギトリ法解析を進めていく第一歩です。
これまで何度も言葉として登場している走時曲線ですが、あまり馴染みがないと思います。
走時曲線とは、起振ごとの初動読取値を、横軸を距離(測点)、縦軸を時間(初動読取値)としてプロットしたグラフになります。
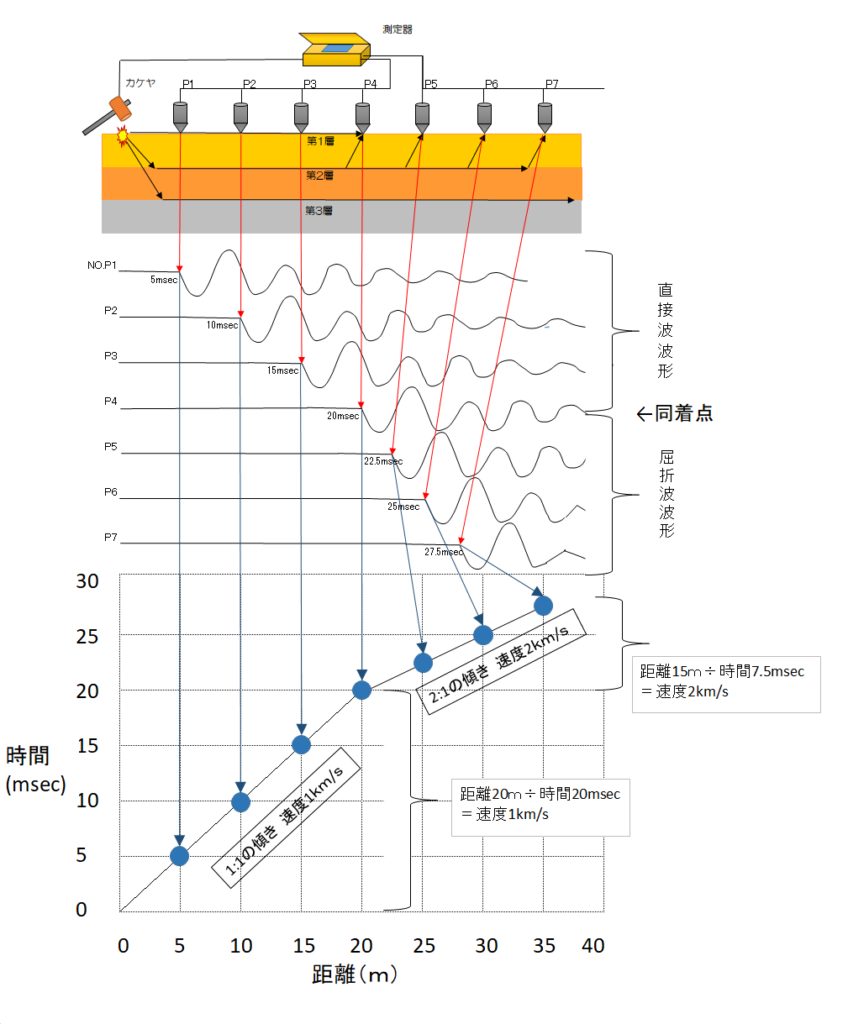
上図は、7ヶの地震計を5m間隔で設置し、0m地点で起振した際の初動読み取りと、その読取値を走時曲線にした模式図です。
初動読取と走時曲線の相関が理解しやすいでしょうか。
さて、これで何が分かるのか?そもそもなぜ走時曲線を作成するのか?というと、弾性波探査の屈折法解析は多くの計算式を用いた難解なものであるため、それを図式解法で単純化し視覚的に分かりやすくするためです。
地盤の硬軟は、地盤を伝わる弾性波の速度で表すので、速度値を求めるのが走時曲線の第一の目的です。速度を求めるには「距離÷時間=速度」の計算をしなくてはなりませんが、横軸=距離、縦軸=時間のグラフの傾きは速度になることから、図上の傾きに定規を当てるだけで速度を求めることができます。
上図を例に用いると、起振点0mから地震計P4までは同じ角度の傾きです。
この傾きに定規をあてると、縦横1マスずつ 1:1の角度であり、速度は1(km/s)となります。
計算では、距離20mでかかった時間は20msec。20m÷20msec=1km/s と、求まります。
さて、P4から先は傾きが変わっています。波が、表層とは速度値の異なる地層を伝わっているためです。
このP4が、表層を伝播する直接波と、下部の硬い層からの屈折波とが同着する地点です。
P1~P4は直接波が先着、P4~P7は屈折波が先着しているということです。
では先程と同様に、傾きに定規をあてると横2マス・縦1マス 2:1の角度であり、速度は2(km/s)となります。
計算では、P4(20m)からP7(35m)まで距離15mで、かかった時間は7.5msec。15m÷7.5msec=2km/s と、求まります。
各速度値を上図にあてはめると、第1層はVp=1km/s、第2層はVp=2km/sであると解析されました。
(厳密に言えば、まだこの段階では真の速度値ではありません)
今回は分かりやすくするため受振点・起振数はごく少数で、地盤モデルも単純な水平2層構造ですが、実際には受振点は数十~数百に及び、起振点も多くなります。地形の変化や地層の数・形状ももっと複雑です。
これらを全て計算すると膨大で難解な作業になりますが、図式解法なら迅速かつ簡便に速度を求めることができます。
ここまでで速度値が求まりましたが、さらに速度層の数、各速度層の速度値、層厚、形状まで、走時曲線の図上で解析していきます。
走時曲線は、屈折法弾性波探査・ハギトリ法解析の要といえるのです。



